Here’s what the .T in NumPy means:
.T is the returned transposed array with its axes permuted that is used in NumPy.
It is the same as calling self.transpose().
When you use .T, you must have at least 2 arrays to work with.
Having only 1 array is ineffective.
This is a standard matrix transpose for a 2-D array.
So if you want to learn all about the meaning of .T in NumPy in Python, then this article is for you.
Let’s jump right into it!

How Is .Transpose() Used In NumPy?
When using .transpose() in NumPy, you’re essentially changing how you look at the array.
Remember it needs to be a 2D array or bigger in order for transpose to work.
Once called, transpose() will reverse or permute the array on its axes.
Take a look at the image below.
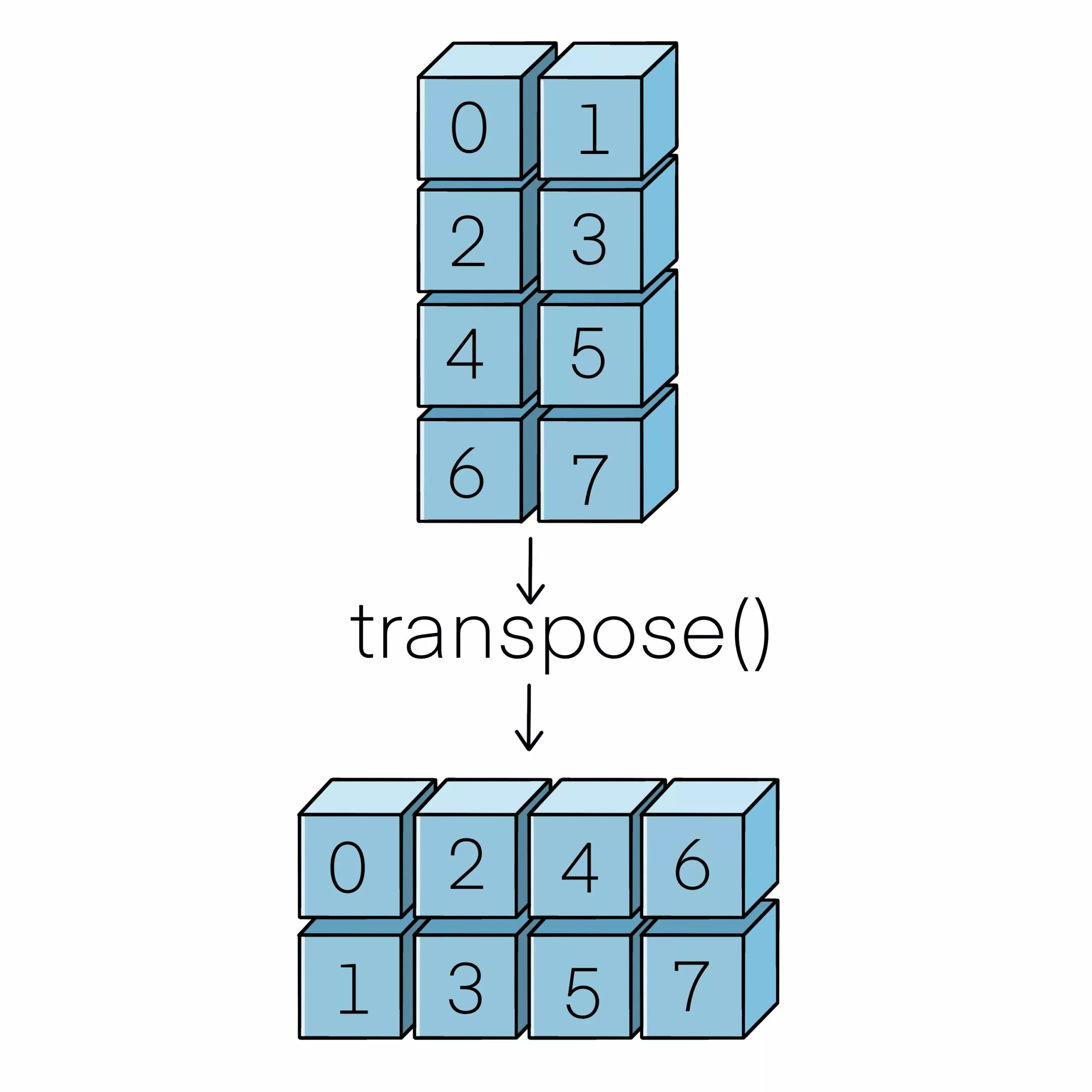
You have 2 stacks of blocks from 0-7 in front of you.
Once you have called transpose(), the blocks have changed!
No longer are they standing up but laying down on their side!
You still have all 8 blocks(0-7) but their position has changed.
It still reads 0-7 in order.
Since multidimensional arrays in NumPy are fixed-sized, even transposed, the ndarray has the same number of items.
All I did was change the group sizes.
Instead of now having 4 groups of 2, I now have 2 groups of 4.
If I didn’t have a 2D array, it would return the only ndarray available with no changes.
The ndim or the number of array dimensions must be >= 2, else nothing happens.
How Is a Transposed Array in NumPy Reshaped? (2 Methods)
As you know with Python and so for NumPy, you can stack methods on top of one another to change the outcome of the output.
In NumPy, you have 2 methods called .shape() and .reshape() respectively.
Not to confuse the 2 of them together.
You can use .shape() and .reshape() in order to .shape()
#1 .shape()
Using the .shape() method the elements of the shape are returned as a tuple giving the lengths of the corresponding array dimensions.
An array can be 1D, 2D, or 3D as far as shape.
Although it is usually used to get the current shape of an array, you can also use it to reshape an array in place.
This is done by assigning a tuple of array dimensions to it.
#2 .reshape()
When you are reshaping a ndarray using .reshape(), the new shape must be compatible with the one you are reshaping.
Look at the illustration below, to see the data get reshaped with the data actually being changed.
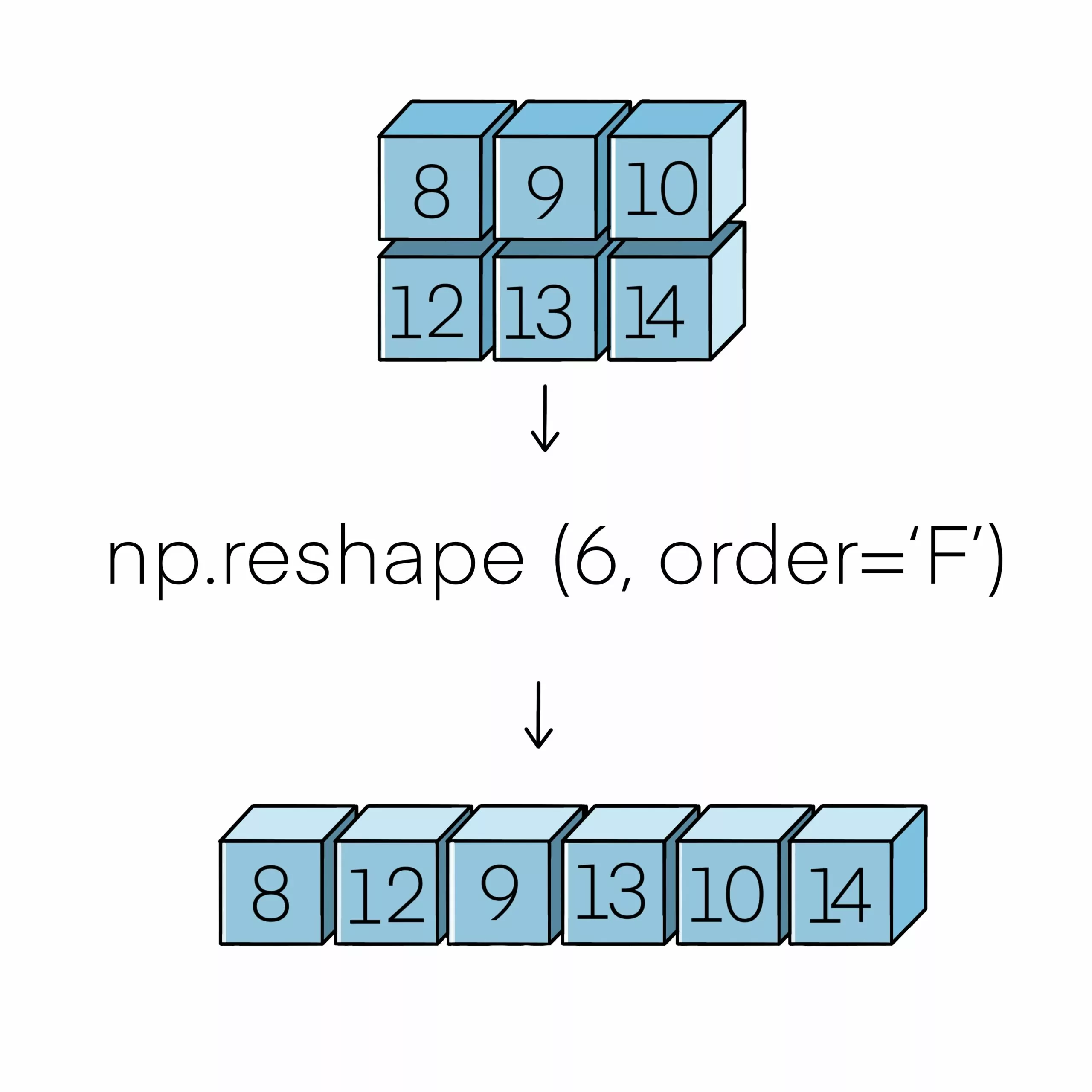
It takes 2 key arguments, the array to be reshaped and the new shape.
The order keyword gives the index the ordering of both the values from the variable and then places those values into an output array.
The ‘F’ means to read/write the elements using Fortran-like index order, with the first index changing fastest, and the last index changing slowest.
Think of it this way, reshaping is first raveling the array in the used index order, then inserting the elements from the raveled array into the new array.
The index order is the same as using the same kind of index order as was used for the raveling.
A new view object if possible will be created; if not then it will be a copy.
There is no guarantee either of the memory layouts, whether it is C or Fortran contiguous of said returned array.
What Similar Methods Can Be Used Instead of NumPy’s Transpose? (2 Techniques)
There are 2 other methods that can be used in place of the .transpose() method in NumPy.
You could use either the method .moveaxis or the method .swapaxes() instead of .transpose().
Each of these three approaches affects the array in a different way.
#1 .moveaxis()
When you use .moveaxis(), you will need 3 parameters in order to move the axes of an array to new positions.
The first parameter is the array with the array that should be reordered, the second parameter is the source or the original positions of axes to move, which must be unique and the third parameter is the destination of where those axes for each of those original axes, these must also be unique.
What is returned is an array with the moved axes.
#2 .swapaxes()
When you use .swapaxes(), you will need 3 parameters in order to interchange the axes of 2 arrays.
The first parameter is the input array, the second parameter is the first axis and the third parameter is the second axis.
If the input array is a ndarray, then a view of that array is returned.
Otherwise, a new array is created and output to the screen.
Below is an example of all 3 methods being used with their outcomes.
np.transpose(x).shape
(5, 4, 3)
np.swapaxes(x, 0, -1).shape
(5, 4, 3)
np.moveaxis(x, [0, 1], [-1, -2]).shape
(5, 4, 3)
np.moveaxis(x, [0, 1, 2], [-1, -2, -3]).shape
(5, 4, 3)
What Are Ndim Arrays in NumPy?
Ndim arrays or n-dimensional arrays are fixed-sized multidimensional arrays used in NumPy as a container of items of the same type and size.
It’s the number of dimensions in an array is determined by its shape.
The shape is N non-negative integers, specifying the sizes of each dimension.
Since different ndarrays can share the same data, any changes made in one ndarray can be visible in another one.
This means you can use one array to “view” another array and the data being taken care of is in the “base” ndarray.
Just like with Python’s other container types, you can not only access but also modify the information inside of a ndarray through slicing and indexing alongside the methods and attributes used for a ndarray.
Viewing memory owned by Python strings and objects implementing the buffer or array interfaces can also be done with ndarrays.
How Are Ndarrays and Array Attributes Constructed In NumPy?
There are 2 ways that you can construct ndarrays in NumPy.
The first way is to use the low-level ndarray constructor like this one here or it can be constructed using the Array creation routines detailed here.
All Array attributes reflect information that is intrinsic to the array itself.
Generally, accessing an array through its attributes allows you to get and sometimes set intrinsic properties of the array without creating a new array.
The exposed attributes are the core parts of an array and only some can be reset meaningfully without creating a whole new array.
There is a lot more to learn when it comes to constructing ndarrays and their attributes.
I would encourage you to look at not only the .T in NumPy but to also study the Array Creation routines.
You will learn to build all kinds of different arrays to manipulate data with, build matrices, and create a pictorial presentation!
It’s totally worth looking into if you want to know more about NumPy and its Array Creation Routines to better understand .T in NumPy.

